Data Structure and algorithm

 

Pre requisites 

you must have basic knowledge of C and C++ programming language

we will be learning about about

  • run time analysis
  • omega notation
  • big O notation
  • theta notation
  • time complexity
  • array data structures
  • linked list data structure
  • stack
  • Queue
  • Tree
  • sorting algorithms
  • Recursion
  • Dynamic Programming
  • Hash Table
  • Graph

Run time Analysis

Run time analysis is an estimate of increasing the run time of an algorithm as its input grows

we should learn this to measure the efficiency of the algorithm.

There are 2 factor for run time analysis

1. Time factor- The number of operations required for a particular algorithm

2. Space factor- The amount of memory used by an algorithm

Time factor is called time complexity which measure the number of  operation requires for particular operations

The time complexity is not about timing with a clock how long the algorithm takes. Instead how many operations are executed. The number of instruction executed by a program is affected by the size of the input. Grate computer(high configuration) will work faster. So this complexity depends on power of CPU.

Space factor is called space complexity which measure the amount of memory used by an algorithm


Notation for Run time analysis

1. Omega Notation -Ω(n) best case

2. Big O notation -  O(n) worst case

3. Theta notation-   θ(n) average case

Mostly Big O notation is used

1. Omega Notation -Ω(n)

  • this notation gives the lower bound of an algorithm
  • this notation used to measure the best case of an algorithm

2. Big O notation -  O(n)

  • This notation gives the upper bond of an algorithm
  • This notation is used to measure the worst case of an algorithm
3. Theta notation-   θ(n)
  • This notation gives the average of lower and upper bond of an algorithm
  • This notation is used to measure the average vase scenario of an algorithm
for array from 1 to 8

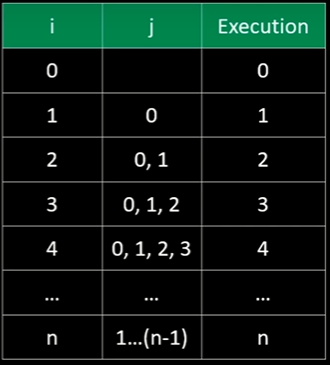
1. Omega Notation -Ω(n) ==> Ω(1)

2. Big O notation -  O(n)==> O(8)

3. Theta notation-   θ(n/2) ==> θ(4)

Example of Run time analysis

Complexity

Name

Example

O(1)

Constant

Adding an element in the front of a linked list

O(log n)

Logarithmic

Searching an element in a sorted array

O(n)

Linear

Searching an element in an unsorted array

O(n log n)

Linear Logarithmic

Merge sort algorithm

O(n2)

Quadratic

Shortest path between 2 cities in a graph

O(n3)

Cubic

Matrix Multiplication

O(2n)

Exponential

Naïve solution of nth Fibonacci problem

O(n!)

Factorial

Naïve solution of Travelling Salesman problem

Big O complexity chart

Common Running times:

  • 1 unit of time is required for arithmetic and Logical operations
  • 1 unit of time is required for assignment and return value
  • 1 unit of time is required for Read and write operations
Constant Time: O(1)
  • Constant time means the running time is constant it's not affected by the size of input
int fn(n):----------------------------O(1)
    int a = n*n;----------------------O(1)
    print(a)---------------------------O(1)
    return a;--------------------------O(1)

all line takes constant time.

Linear Time: O(n)

  • When an algorithm accept n input size , it would perform n operations as well
int[] nums = {1,2,3,4,5,6}-------------O(1)
for(int i=0;i<num.length;n++):-------O(n)
    print(nums[i]);-----------------------O(1)

Logarithmic Time O(log n)
  • Algorithm that has running time 0(log n) is slightly faster than O(n).
  • Example binary search algorithm
binary_search(nums, target):-------T(n)
    left=0;-----------------------------O(1)
    right=len(nums)-1---------------O(1)
    while(left<=right):--------------T(n/2)
        mid=left+(right-left)/2;------O(1)
        if(nums[mid]==target):------O(1)
            return mid;------------------O(1)
        else if(target>num[mid]);----O(1)
            left=mid+1;------------------O(1)
        else:            ---------------------O(1)
            right=mid-1;------------------O(1)
    return -1;----------------------------O(1)



TC: O(log2(n))
SC: O(1)

Linear Logarithmic Time: O(n log n)
  • This algorithm divide the problem into sub problem and then merge them in n time
  • example Merge sort Algorithm
TC: O(n*log(n))
SC: O(n)

Quadratic Time O(n2)
  • Bubble sort algorithm takes quadratic time complexity. In other words a loop inside other loop.
for(i=0;i<N;i++): ----------------------O(n)
    for(int j=0;j<N;j++) ----------------O(n)
        statements;------------------------O(1)

Cubic Time O(n3)
  • It has the same principle as Quadratic Time O(n2)
Exponential Time O(2n)
  • It is very slow algorithm as input grow, if n=100000, T(n) would be 2100000. we can consider brute force algorithm. Example Backtracking Algorithm
Factorial Time O(n!)
  • It is the slowest algorithm

Why should we learn Complexity Analysis?
For input size n=10 bother liner search and binary search take similar time
for input size n= 1 billion linear search takes 1 billion ms but binary search takes only 32 ms

So we can optimize our code.


eg1
for(int i=1;i<=n;i++):-----------O(n)
    print(i); ------------------------O(1)

TC: O(n)
SC: O(1)

eg2
for(int i=1;i<=n;i+=2):-----------O(n/2)
    print(i); ------------------------O(1)

TC: O(n)
SC: O(1)

for(int i=1;i<=n;i+=20):-----------O(n/20)
    print(i); ------------------------O(1)

TC: O(n)
SC: O(1)

eg3

for(int i0;i<n;i++): -----------O(n)
    for(int j=0;j<i;j++): --------O(n)
        print(j); --------------------O(1)


1+2+3+4+....+n= n(n+1)/2 = (n^2+n)/2


TC: O(n2)
SC: O(1)

eg4
p=0 ------------------------------O(n)

for(int i=1;p<=n;i+=p): --------(√n)

    //statements; ---------------O(1)



let assume, p>n
p=1+2+3+4+....k = K(k+1)/2 = (K^2+K)/2

TC:O(√n)
SC:O(1)

eg5

for(int i=1;i<n;i*=2):
    statements;

suppose, i>=n

=> i=2k
so, 2k >=n
=> log <sub>2</sub> (2k)=log<sub>2<sub>(n)
=>k=log<sub>2</sub>(n)


TC:O(log<sub>2</sub>(n))
SC: O(1)


Data Structures and Algorithms:

Let's clear up our basics with these terms before deep diving into DSA.  Data Structures and Algorithms are two different things.

Data Structures –  These are like the ingredients you need to build efficient algorithms. These are the ways to arrange data so that they (data items) can be used efficiently in the main memory. Examples: Array, Stack, Linked List, and many more. You don't need to worry about these names. These topics will be covered in detail in the upcoming tutorials.

Algorithms – Sequence of steps performed on the data using efficient data structures to solve a given problem, be it a basic or real-life-based one.  Examples include: sorting an array.

Some other Important terminologies:

  1. Database – Collection of information in permanent storage for faster retrieval and updating. Examples are MySql, MongoDB, etc.
  2. Data warehouse – Management of huge data of legacy data( the data we keep at a different place from our fresh data in the database to make the process of retrieval and updation fast) for better analysis.
  3. Big data – Analysis of too large or complex data, which cannot be dealt with the traditional data processing applications.

Memory Layout of C Programs:

  • When the program starts, its code gets copied to the main memory.
  • The stack holds the memory occupied by functions. It stores the activation records of the functions used in the program. And erases them as they get executed.
  • The heap contains the data which is requested by the program as dynamic memory using pointers.
  • Initialized and uninitialized data segments hold initialized and uninitialized global variables, respectively.

Take a look at the below diagram for a better understanding:

This is just the beginning. Data Structures and Algorithms are not new concepts. If you have done programming in any language like C, you must have come across  Arrays – A data structure. And algorithms are just sequences of processing steps to solve a problem.

Time Complexity and Big O Notation

Time Complexity is the study of the efficiency of algorithms. It tells us how much time is taken by an algorithm to process a given input.

 

Putting it simply, Big O stands for ‘order of’ in our industry, 

but this is pretty different from the mathematical definition of the big O. 

Big O in mathematics stands for all those complexities our program runs in. 

But in industry, we are asked the minimum of them. So is a subtle difference.

What is a Big O?

Putting it simply, big O stands for ‘order of’ in our industry, but this is pretty different from the mathematical definition of the big O. Big O in mathematics stands for all those complexities our program runs in. But in industry, we are asked the minimum of them. So this was a subtle difference.

Visualizing Big O:

If we were to plot O(1) and O(n) on a graph, they would look something like this:

So, this was the basics of time complexities. You don't have to worry about things passing you by.



Asymptotic Notations: Big O, Big Omega and Big Theta Explained (With Notes)

Asymptotic notation gives us an idea about how good a given algorithm is compared to some other algorithm.

Now let's look at the mathematical definition of 'order of.' Primarily there are three types of widely used asymptotic notations.

  1. Big oh notation ( O )
  2. Big omega notation ( Ω )
  3. Big theta notation ( θ ) – Widely used one

Big oh notation ( O ):

  • Big oh notation is used to describe an asymptotic upper bound.
  • Mathematically, if f(n) describes the running time of an algorithm; f(n) is O(g(n)) if and only if there exist positive constants c and n° such that:
    0 ≤ f(n) ≤ c g(n)        for all n ≥ n°.
  • Here, n is the input size, and g(n) is any complexity function, for, e.g. n, n2, etc. (It is used to give upper bound on a function)
  • If a function is O(n), it is automatically O(n2) as well! Because it satisfies the equation given above.

 Graphic example for Big oh ( O ):

Big Omega Notation ( Ω ):

  • Just like O notation provides an asymptotic upper bound, Ω notation provides an asymptotic lower bound. 
  • Let f(n) define the running time of an algorithm; f(n) is said to be Ω (g(n)) if and only if there exist positive constants  c and n° such that:
    0 ≤ c g(n) ≤ f(n)        for all n ≥ n°.

  • It is used to give the lower bound on a function.

  • If a function is Ω (n2) it is automatically Ω (n) as well since it satisfies the above equation.

 Graphic example for Big Omega (Ω):

Big Omega Notation ( Ω ):

  • Just like O notation provides an asymptotic upper bound, Ω notation provides an asymptotic lower bound. 
  • Let f(n) define the running time of an algorithm; f(n) is said to be Ω (g(n)) if and only if there exist positive constants  c and n° such that:

Mathematically,

Merging both the equations, we get:

 0  ≤ c2 g(n)  ≤  f(n) ≤ c1 g(n)      ∀    n ≥ no.

The equation simply means that there exist positive constants c1 and c2 such that f(n) is sandwiched between c2 g(n) and c1 g(n). 

Graphic example of Big theta ( θ ):

Which one of these to use?

Big theta provides a better picture of a given algorithm's run time, which is why most interviewers expect you to answer in terms of Big theta when they ask "order of" questions. And what you provide as the answer in Big theta, is already a Big oh and a Big omega. It is recommended for this reason.

 Quick Quiz: Prove that n2+n+1 is O(n3), Ω(n2), and θ(n2) using respective definitions.

Hint: You can approach this both graphically, making some rough graphs and mathematically, finding valid constants c1 and c2.

Increasing order of common runtimes:

Below mentioned are some common runtimes which you will come across in your coding career.

So, this was all about the asymptotic notations.



Comments

Post a Comment